Trees algorithm

Trees in C++

What is Binary Tree?
A tree whose elements have at most 2 children is called a binary tree. Since each element in a binary tree can have only 2 children, we typically name them the left and right child.

Binary Tree Representation in C/C++: A tree is represented by a pointer to the topmost node in tree. If the tree is empty, then value of root is NULL.
A Tree node contains following parts.

Data

Pointer to left child

Pointer to right child

In C/C++, we can represent a tree node using structures. Below is an example of a tree node with an integer data.

struct node
{
	int data;
	struct node* left;
	struct node* right;
};

Main applications of trees include:
1. Manipulate hierarchical data.
2. Make information easy to search (see tree traversal).
3. Manipulate sorted lists of data.
4. As a workflow for compositing digital images for visual effects.
5. Router algorithms
6. Form of a multi-stage decision-making (see business chess).

#include <bits/stdc++.h>
using namespace std;

struct Node {
	int data;
	struct Node* left;
	struct Node* right;

	// val is the key or the value that
	// has to be added to the data part
	Node(int val)
	{
		data = val;

		// Left and right child for node
		// will be initialized to null
		left = NULL;
		right = NULL;
	}
};

int main()
{

	/*create root*/
	struct Node* root = new Node(1);
	/* following is the tree after above statement

			1
			/ \
		NULL NULL
	*/

	root->left = new Node(2);
	root->right = new Node(3);
	/* 2 and 3 become left and right children of 1
					1
				/ \
				2	 3
			/ \	 / \
			NULL NULL NULL NULL
	*/

	root->left->left = new Node(4);
	/* 4 becomes left child of 2
			1
			/	 \
		2	 3
		/ \	 / \
		4 NULL NULL NULL
		/ \
	NULL NULL
	*/

	return 0;
}

Tree Traversals Algorithm.

Unlike linear data structures (Array, Linked List, Queues, Stacks, etc) which have only one logical way to traverse them, trees can be traversed in different ways.

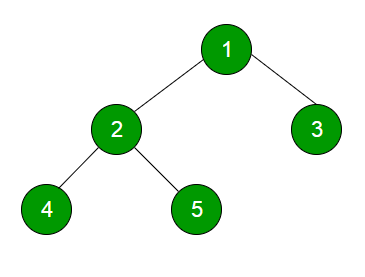
Example Tree

Depth First Traversals (DFS) Algorithm

(a) Inorder (Left, Root, Right) : 4 2 5 1 3

Uses of Inorder
In case of binary search trees (BST), Inorder traversal gives nodes in non-decreasing order. To get nodes of BST in non-increasing order, a variation of Inorder traversal where Inorder traversal s reversed can be used.

(b) Preorder (Root, Left, Right) : 1 2 4 5 3

Uses of Preorder
Preorder traversal is used to create a copy of the tree. Preorder traversal is also used to get prefix expression on of an expression tree.

Algorithm Inorder(tree)

Traverse the left subtree, i.e., call Inorder(left-subtree)

Visit the root.

Traverse the right subtree, i.e., call Inorder(right-subtree)

// C++ program for different tree traversals
#include <iostream>
using namespace std;

/* A binary tree node has data, pointer to left child
and a pointer to right child */


struct Node {
	int data;
	struct Node *left, *right;
	Node(int data)
	{
		this->data = data;
		left = right = NULL;
	}
};


/* Given a binary tree, print its nodes in inorder*/
void printInorder(struct Node* node)
{
	if (node == NULL)
		return;

	/* first recur on left child */
	printInorder(node->left);

	/* then print the data of node */
	cout << node->data << " ";

	/* now recur on right child */
	printInorder(node->right);
}


/* Driver program to test above functions*/
int main()
{
	struct Node* root = new Node(1);
	root->left = new Node(2);
	root->right = new Node(3);
	root->left->left = new Node(4);
	root->left->right = new Node(5);

	cout << "\nInorder traversal of binary tree is \n";
	printInorder(root);

	return 0;
}

Algorithm Preorder(tree)

Visit the root.

Traverse the left subtree, i.e., call Preorder(left-subtree)

Traverse the right subtree, i.e., call Preorder(right-subtree)

// C++ program for different tree traversals
#include <iostream>
using namespace std;

/* A binary tree node has data, pointer to left child
and a pointer to right child */

struct Node {
	int data;
	struct Node *left, *right;
	Node(int data)
	{
		this->data = data;
		left = right = NULL;
	}
};


/* Given a binary tree, print its nodes in preorder*/
void printPreorder(struct Node* node)
{
	if (node == NULL)
		return;

	/* first print data of node */
	cout << node->data << " ";

	/* then recur on left sutree */
	printPreorder(node->left);

	/* now recur on right subtree */
	printPreorder(node->right);
}

/* Driver program to test above functions*/
int main()
{
	struct Node* root = new Node(1);
	root->left = new Node(2);
	root->right = new Node(3);
	root->left->left = new Node(4);
	root->left->right = new Node(5);

	cout << "\nPreorder traversal of binary tree is \n";
	printPreorder(root);


	return 0;
}

Algorithm Postorder(tree)

Traverse the left subtree, i.e., call Postorder(left-subtree)

Traverse the right subtree, i.e., call Postorder(right-subtree)

Visit the root.

// C++ program for different tree traversals
#include <iostream>
using namespace std;

/* A binary tree node has data, pointer to left child
and a pointer to right child */

struct Node {
	int data;
	struct Node *left, *right;
	Node(int data)
	{
		this->data = data;
		left = right = NULL;
	}
};

/* Given a binary tree, print its nodes according to the
"bottom-up" postorder traversal. */

void printPostorder(struct Node* node)
{
	if (node == NULL)
		return;

	// first recur on left subtree
	printPostorder(node->left);

	// then recur on right subtree
	printPostorder(node->right);

	// now deal with the node
	cout << node->data << " ";
}

/* Driver program to test above functions*/
int main()
{
	struct Node* root = new Node(1);
	root->left = new Node(2);
	root->right = new Node(3);
	root->left->left = new Node(4);
	root->left->right = new Node(5);

	cout << "\nPostorder traversal of binary tree is \n";
	printPostorder(root);

	return 0;
}

Breadth First or Level Order Traversal (BFS) Algorithm

Breadth First Traversal: 1 2 3 4 5

Implementation Algorithm.

printLevelorder(tree)

Create an empty queue q

temp_node = root /start from root/

Loop while temp_node is not NULL

print temp_node->data.

Enqueue temp_node’s children (first left then right children) to q

Dequeue a node from q.

/* C++ program to print level
	order traversal using STL */
#include <bits/stdc++.h>
using namespace std;

// A Binary Tree Node
struct Node
{
	int data;
	struct Node *left, *right;
};

// Iterative method to find height of Binary Tree
void printLevelOrder(Node *root)
{
	// Base Case
	if (root == NULL) return;

	// Create an empty queue for level order traversal
	queue<Node *> q;

	// Enqueue Root and initialize height
	q.push(root);

	while (q.empty() == false)
	{
		// Print front of queue and remove it from queue
		Node *node = q.front();
		cout << node->data << " ";
		q.pop();

		/* Enqueue left child */
		if (node->left != NULL)
			q.push(node->left);

		/*Enqueue right child */
		if (node->right != NULL)
			q.push(node->right);
	}
}

// Utility function to create a new tree node
Node* newNode(int data)
{
	Node *temp = new Node;
	temp->data = data;
	temp->left = temp->right = NULL;
	return temp;
}

// Driver program to test above functions
int main()
{
	// Let us create binary tree shown in above diagram
	Node *root = newNode(1);
	root->left = newNode(2);
	root->right = newNode(3);
	root->left->left = newNode(4);
	root->left->right = newNode(5);

	cout << "Level Order traversal of binary tree is \n";
	printLevelOrder(root);
	return 0;
}

Output

Level Order traversal of binary tree is 
1 2 3 4 5

Written on April 19, 2021